⓪本記事の3行要約
- 『野球のOR』の計算過程をPython上で再現したい。
- 均一な打者などの現実に即さない仮定をおいた。
- 各アウト数・塁状況組の期待得点・得点確率を算出した。
➀『野球のOR』について
-(1)『野球のOR』とは
『野球のOR』とは1979年に公開されたOR(オペレーションズリサーチ)分野の論文です。ここでは、OR手法を野球に応用することで作戦の効果やプレーの価値を分析しています。具体的には、デソポ=レフコヴィッツの得点インデックスに似た方法から状況別の期待得点と得点確率(以下、理論値)を求めることで、アウトカウント・塁状況と1イニングにおける各理論値の関係を明らかにしました。そして、この論文ではそれらの計算結果から各作戦やプレーの価値を議論しています。
-(2)本記事の目的
本記事では、『野球のOR』における各理論値の計算方法をPython上で再現することで、これから行う分析のベンチマークにしたいと思います。なお、『野球のOR』は現実に即さない仮定を前提に分析するため、その結果が全て正しいものだと受け入れられません。これらの極端な仮定については次章にて詳説します。
➁『野球のOR』における諸仮定
-(1)野球とORの良好な関係
まず、OR手法の応用において野球の打席ごとにプレーが途切れるという性質はとても好都合です。なぜなら、この特徴によって野球の各プレーはある程度独立しているとみなすことができるからです。前の打者の打席結果が次の打者の打席結果に大きな影響を与えるとは考えられないでしょう。そのため、野球とORは非常に相性の良い組み合わせであるといえるのです。
-(2)理想的なモデルとは
このとき、野球とORは好相性ですが必ずしも野球の分析が容易であるとはいえません。野球を完全再現するためには複雑なモデルが必要であり、モデルが複雑になれば分析の難易度は上がります。また、複雑なモデルの分析結果は解釈困難に陥ることもしばしばです。
しかし、過度に単純なモデルから得られる結論に意味はありません。コインの表裏から野球の勝敗をシミュレートする分析から得られるものは少ないでしょう。そのため、再現度と複雑さのバランスがとれたモデルを考える必要があります。
-(3)仮定の導入
そこで、いくつかの仮定により野球を単純化したモデルを考えましょう。『野球のOR』では次の仮定をおいています。おおよそ、野球を野球盤のように捉えたモデルです。唯一、2塁走者が単打で生還できる点が野球盤のルールと異なります。なお、この仮定は各理論値の算出を容易にする一方で、今後の様々な分析における大きな障害となります。
[仮定]
- 仮定➀:打順を構成する選手の打撃能力は均一である。
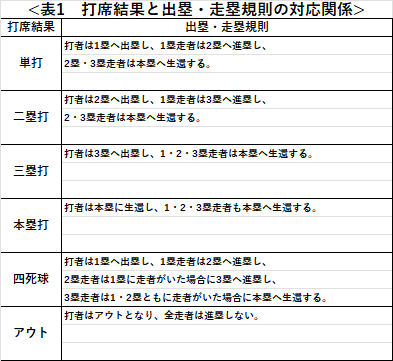
- 仮定➁:打席結果は表1の6種類のみであり、成績に従い確率的に決定される。
- 仮定③:走塁は打席結果のみに従い、表1の通りに対応する。
- 仮定④:以上の仮定で想定されないプレー(失策等)は無視する。
③仮定より導かれる諸法則
以上の仮定によって、野球はとても単純な競技として分析できるようになりました。その結果、このモデルでは現実の野球で成立する諸法則だけでなく、現実では成立しない以下の法則が成立するようになります。
[法則]
- 法則➀:求めるべき期待得点・得点確率は24通りである。
- 法則➁:k人の走者がいる場面でn-k+4回出塁すれば必ずn+1得点できる。
- 法則③:m回出塁時にn得点する条件付き確率はアウト数に依存しない。
- 法則④:走者なし時にn(n>0)得点する攻撃展開は走者k人時にn+k得点できる。
- 法則⑤:走者2塁と走者3塁や走者12塁と走者13塁は同値である。
④分析の下準備
-(1)下準備の方向性
本記事の最終目的は各理論値の計算なのですが、これらを一度に求めることは困難です。しかし、各条件において一つずつ求めるのも生産的とは言えません。そこで、何らかの場合分けを用いることで状況を整理し、効率的に計算を行いたいと思います。なお、本章の内容は少し難解なため読み飛ばして頂いて問題ありません。
-(2)出塁数と条件付き確率
『野球のOR』では出塁数による場合分けを利用して各理論値を計算しています。これによって、各理論値の算出時に法則➁③を利用できるようになります。具体的には、走者k人である特定の状況からm回出塁することでn得点する条件付き確率が求まれば、m>3-kを満たすmにおいて必ず得点が記録されること(法則➁)を利用して計算量を減らすことができるのです。このとき、この条件付き確率は次のように求まります。
| ・P(出塁数=m⋂得点=n|iアウト,塁状況j) | = | P(出塁数=m|iアウト,塁状況j)×P(得点=n|iアウト,m出塁,塁状況j) | |
また、特定の状況からm回出塁する確率は以下の通り簡単に求まります。
| ・P(出塁数=m|iアウト,塁状況j) | = | m+2-iC2-i(出塁する確率)m×(アウトになる確率)3-i | |
-(3)新たな問題点
以上より、あとは特定の状況からイニング終了までにm回出塁した時にn得点する条件付き確率を求めれば十分です。しかし、得点と出塁数の組み合わせは無限に存在するため、この条件付き期待値を全て求めることはできません。また、これではこの条件付き確率がアウト数に依存しないこと(法則③)を利用しても意味がありません。
-(4)『野球のOR』における解決策
では、『野球のOR』ではどうしているのでしょうか。⑤⑥の議論を先に確認すれば明らかですが、実際に求める必要のある条件付き確率は8通りしかありません。しかも、それらの条件付き期待値は以下の通り簡単に求まります。
[最低限必要な条件付き確率]
| ・P(得点=0|1出塁,走者なし) | = | P(走者1塁で残塁|1出塁,走者なし)+P(走者2塁で残塁|1出塁,走者なし)+ P(走者3塁で残塁|1出塁,走者なし) | |
| ・P(得点=0|2出塁,走者なし) | = | P(走者12塁で残塁|2出塁,走者なし)+P(走者23塁で残塁|2出塁,走者なし)+ P(走者13塁で残塁|2出塁,走者なし) | |
| ・P(得点=0|3出塁,走者なし) | = | P(走者満塁で残塁|3出塁,走者なし) | |
| ・P(得点=0|1出塁,走者1塁) | = | P(走者12塁で残塁|1出塁,走者1塁)+P(走者23塁で残塁|1出塁,走者1塁) | |
| ・P(得点=0|2出塁,走者1塁) | = | P(走者満塁で残塁|2出塁,走者1塁) | |
| ・P(得点=0|1出塁,走者2塁) | = | P(走者12塁で残塁|1出塁,走者2塁) | |
| ・P(得点=0|2出塁,走者2塁) | = | P(走者満塁で残塁|2出塁,走者2塁) | |
| ・P(得点=0|1出塁,走者12塁) | = | P(走者満塁で残塁|1出塁,走者12塁) | |
⑤得点確率の計算
-(1)不要な計算を排除する
以上の議論より、求めるべき得点確率は24通りです(法則①)が、同値な塁状況があるため実際に必要な値は18通りです(法則⑤)。さらに、k人の走者がいる場面で無得点となる確率を求める際には、4-k回以上出塁した場合を考慮する必要がありません(法則➁)。
-(2)得点確率を計算する
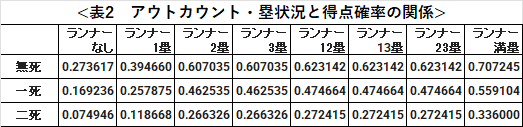
以上を踏まえると、各アウトカウント・塁状況における得点確率の計算式は以下の通りとなります。また、『野球のOR』と同条件において算出された得点確率は表2の通りであり、論文の分析結果とほぼ同じものとなっています。
[得点確率]
| ・P(得点≧1|iアウト,走者なし) | = | 1−P(出塁数=0|iアウト)-P(出塁数=1⋂得点=0|iアウト,走者なし)- P(出塁数=2⋂得点=0|iアウト,走者なし)- P(出塁数=3⋂得点=0|iアウト,走者なし) | |
| ・P(得点≧1|iアウト,走者1塁) | = | 1−P(出塁数=0|iアウト)-P(出塁数=1⋂得点=0|iアウト,走者1塁)- P(出塁数=2⋂得点=0|iアウト,走者1塁) | |
| ・P(得点≧1|iアウト,走者3塁) | = | P(得点≧1|iアウト,走者2塁) |
| ・P(得点≧1|iアウト,走者2塁) | = | 1−P(出塁数=0|iアウト)-P(出塁数=1⋂得点=0|iアウト,走者2塁)- P(出塁数=2⋂得点=0|iアウト,走者2塁) | |
| ・P(得点≧1|iアウト,走者12塁) | = | 1−P(出塁数=0|iアウト)-P(出塁数=1⋂得点=0|iアウト,走者12塁) | |
| ・P(得点≧1|iアウト,走者13塁) | = | P(得点≧1|iアウト,走者12塁) | |
| ・P(得点≧1|iアウト,走者23塁) | = | P(得点≧1|iアウト,走者13塁) | |
| ・P(得点≧1|iアウト,走者満塁) | = | 1−P(出塁数=0|iアウト) | |
⑥期待得点の計算
-(1)不要な計算の排除
⑤の議論と同様に、ここで本来求めるべき期待得点は24通りです(法則①)が、同値な塁状況があるため実際に必要な値は18通りです(法則⑤)。さらに、得点確率が分かっている場合には走者なし時の3通りを計算するだけで全ての期待得点を求めることができます(法則④)。
-(2)期待得点の計算
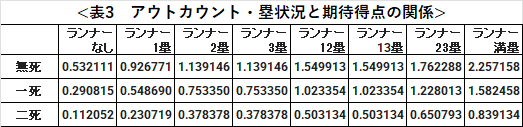
以上を踏まえて、各アウトカウント・塁状況における期待得点の計算式は以下の通りとなります。また、『野球のOR』と同条件において算出された期待得点は表3の通りであり、論文の分析結果とほぼ同じものとなっています。
[期待得点]
| ・E(得点|iアウト,走者なし) | = | E(出塁数|iアウト)−E(残塁数|iアウト) | |
| ・E(得点|iアウト,走者1塁) | = | E(得点|iアウト,走者なし)+E(1塁走者の得点|iアウト,走者1塁) | |
| ・E(得点|iアウト,走者2塁) | = | E(得点|iアウト,走者なし)+E(2塁走者の得点|iアウト,走者2塁) | |
| ・E(得点|iアウト,走者3塁) | = | E(得点|iアウト,走者なし)+E(3塁走者の得点|iアウト,走者3塁) | |
| ・E(得点|iアウト,走者12塁) | = | E(得点|iアウト,走者なし)+E(1塁走者の得点|iアウト,走者1塁)+ E(2塁走者の得点|iアウト,走者12塁) | |
| ・E(得点|iアウト,走者13塁) | = | E(得点|iアウト,走者12塁) | |
| ・E(得点|iアウト,走者23塁) | = | E(得点|iアウト,走者なし)+E(2塁走者の得点|iアウト,走者2塁)+ E(3塁走者の得点|iアウト,走者23塁) | |
| ・E(得点|iアウト,走者満塁) | = | E(得点|iアウト,走者なし)+E(1塁走者の得点|iアウト,走者1塁)+ E(2塁走者の得点|iアウト,走者12塁)+E(3塁走者の得点|iアウト,走者満塁) | |
⑦おわりに
-(1)まとめ
今回は『野球のOR』における期待得点と得点確率の算出をPythonにより再現しました。現実から大きく乖離するほどに非常に簡単なモデルである一方で、意外にも計算方法が直感的には分かりにくく難しい内容であったかと思います。
-(2)今後の展望
次回は、このモデルを応用することで各作戦の効果を検証しようと思います。また、将来的にはもう少し現実の野球に近く直感的に理解しやすいモデルも紹介する予定です。

コメント
コメントを投稿